Hands-On with Supervised Learning: Linear Regression

Image by Author Basic Overview

Linear regression is the fundamental supervised machine learning algorithm for predicting the continuous target variables based on the input features. As the name suggests it assumes that the relationship between the dependant and independent variable is linear. So if we try to plot the dependent variable Y against the independent variable X, we will obtain a straight line. The equation of this line can be represented by:

Where,

• Y Predicted output.
• X = Input feature or feature matrix in multiple linear regression
• b0 = Intercept (where the line crosses the Y-axis).
• b1 = Slope or coefficient that determines the line's steepness.

The central idea in linear regression revolves around finding the best-fit line for our data points so that the error between the actual and predicted values is minimal. It does so by estimating the values of b0 and b1. We then utilize this line for making predictions.

Implementation Using Scikit-Learn

You now understand the theory behind linear regression but to further solidify our understanding, let's build a simple linear regression model using Scikit-learn, a popular machine learning library in Python. Please follow along for a better understanding.

1. Import Necessary Libraries

First, you will need to import the required libraries.

import os  import pandas as pd  import numpy as np  import matplotlib.pyplot as plt  from sklearn.linear_model import LinearRegression  from sklearn.preprocessing import StandardScaler  from sklearn.metrics import mean_squared_error

2. Analyzing the Dataset

You can find the dataset here. It contains separate CSV files for training and testing. Let’s display our dataset and analyze it before proceeding forward.

# Load the training and test datasets from CSV files  train = pd.read_csv('train.csv')  test = pd.read_csv('test.csv')    # Display the first few rows of the training dataset to understand its structure  print(train.head())

Output:

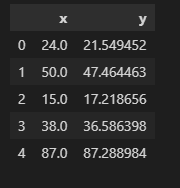
train.head()

The dataset contains 2 variables and we want to predict y based on the value x.

# Check information about the training and test datasets, such as data types and missing values  print(train.info())  print(test.info())

Output:

  RangeIndex: 700 entries, 0 to 699  Data columns (total 2 columns):   #   Column  Non-Null Count  Dtype    ---  ------  --------------  -----     0   x       700 non-null    float64   1   y       699 non-null    float64  dtypes: float64(2)  memory usage: 11.1 KB          RangeIndex: 300 entries, 0 to 299  Data columns (total 2 columns):   #   Column  Non-Null Count  Dtype    ---  ------  --------------  -----     0   x       300 non-null    int64     1   y       300 non-null    float64  dtypes: float64(1), int64(1)  memory usage: 4.8 KB

The above output shows that we have a missing value in the training dataset that can be removed by the following command:

train = train.dropna()

Also, check if your dataset contains any duplicates and remove them before feeding it into your model.

duplicates_exist = train.duplicated().any()  print(duplicates_exist)

Output:

False

2. Preprocessing the Dataset

Now, prepare the training and testing data and target by the following code:

#Extracting x and y columns for train and test dataset  X_train = train['x']  y_train = train['y']  X_test = test['x']  y_test = test['y']  print(X_train.shape)  print(X_test.shape)

Output:

(699, )  (300, )

You can see that we have a one-dimensional array. While you could technically use one-dimensional arrays with some machine learning models, it's not the most common practice, and it may lead to unexpected behavior. So, we will reshape the above to (699,1) and (300,1) to explicitly specify that we have one label per data point.

X_train = X_train.values.reshape(-1, 1)  X_test = X_test.values.reshape(-1,1)

When the features are on different scales, some may dominate the model's learning process, leading to incorrect or suboptimal results. For this purpose, we perform the standardization so that our features have a mean of 0 and a standard deviation of 1.

Before:

print(X_train.min(),X_train.max())

Output:

(0.0, 100.0)

Standardization:

scaler = StandardScaler()  scaler.fit(X_train)  X_train = scaler.transform(X_train)  X_test = scaler.transform(X_test)  print((X_train.min(),X_train.max())

Output:

(-1.72857469859145, 1.7275858114641094)

We are now done with the essential data preprocessing steps, and our data is ready for training purposes.

4. Visualizing the Dataset

It's important to first visualize the relationship between our target variable and feature. You can do this by making a scatter plot:

# Create a scatter plot  plt.scatter(X_train, y_train)  plt.xlabel('X')  plt.ylabel('Y')  plt.title('Scatter Plot of Train Data')  plt.grid(True)  # Enable grid  plt.show()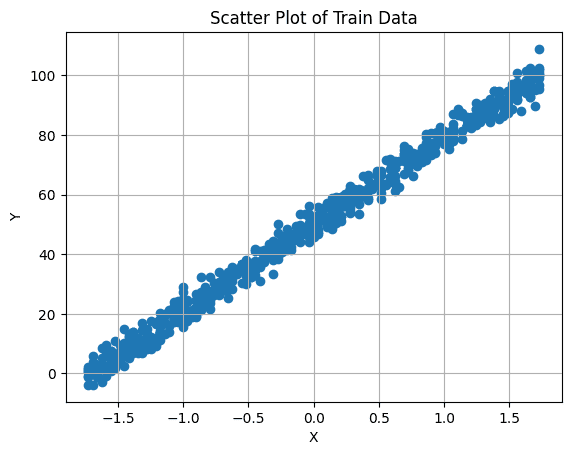  

Image by Author

5. Create and Train the Model

We will now create an instance of the Linear Regression model using Scikit Learn and try to fit it into our training dataset. It finds the coefficients (slopes) of the linear equation that best fits your data. This line is then used to make the predictions. Code for this step is as follows:

# Create a Linear Regression model  model = LinearRegression()    # Fit the model to the training data   model.fit(X_train, y_train)    # Use the trained model to predict the target values for the test data  predictions = model.predict(X_test)    # Calculate the mean squared error (MSE) as the evaluation metric to assess model performance  mse = mean_squared_error(y_test, predictions)  print(f'Mean squared error is: {mse:.4f}')

Output:

Mean squared error is: 9.4329

6. Visualize the Regression Line

We can plot our regression line using the following command:

# Plot the regression line  plt.plot(X_test, predictions, color='red', linewidth=2, label='Regression Line')    plt.xlabel('X')  plt.ylabel('Y')  plt.title('Linear Regression Model')  plt.legend()  plt.grid(True)  plt.show()

Output:

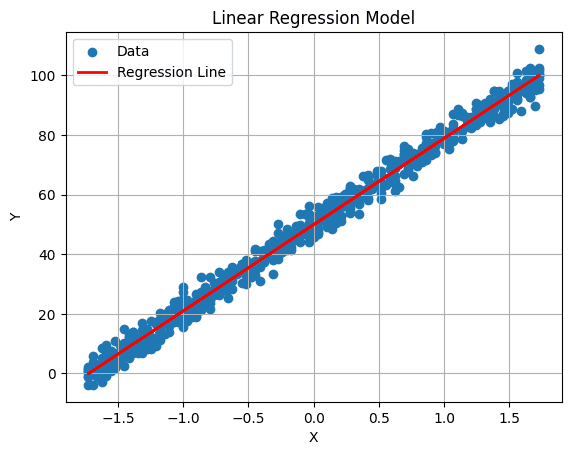
Image by Author Conclusion

That's a wrap! You've now successfully implemented a fundamental Linear Regression model using Scikit-learn. The skills you've acquired here can be extended to tackle complex datasets with more features. It's a challenge worth exploring in your free time, opening doors to the exciting world of data-driven problem-solving and innovation.
Kanwal Mehreen is an aspiring software developer with a keen interest in data science and applications of AI in medicine. Kanwal was selected as the Google Generation Scholar 2022 for the APAC region. Kanwal loves to share technical knowledge by writing articles on trending topics, and is passionate about improving the representation of women in tech industry.

More On This Topic

• Comparing Linear and Logistic Regression
• 3 Reasons Why You Should Use Linear Regression Models Instead of Neural…
• Linear vs Logistic Regression: A Succinct Explanation
• KDnuggets News 22:n12, March 23: Best Data Science Books for Beginners;…
• Linear Regression for Data Science
• Making Predictions: A Beginner's Guide to Linear Regression in Python